Bu yöntem iki ya da daha fazla kaynağı bulunan doğrusal elektrik devrelerine uygulanır.Doğrusal devre, direncin her zaman sabit kaldığı devredir.Her kaynağın bir devreden geçireceği akımların veya oluşturacağı gerilimlerin toplamı, o devrenin akımını veya gerilimini verir.Bu yöntem uygulanırken, devredeki kaynaklar sıra ile devrede bırakılarak , diğerleri devreden çıkartılır. Kaynakları devreden çıkartırken, kaynak gerilim kaynağı ise açılan uçlar kısa devre yapılır.Eğer kaynak akım kaynağı ise açılan uçlar açık devre olarak bırakılır.
İki ya da daha fazla kaynaklı devrelerde, herhangi bir devrenin akımı yada gerilimi , her bir kaynağın meydana getirdiği akım yada gerilimlerin aritmetik toplamıdır.
İki Kaynaklı Gerilim Bölücü :
Aşağıdaki şekildeki devrede, istenen, P noktası ile şase arasındaki gerilim değerinin bulunmasıdır. P noktasındaki gerilimlerin bulunması için, şekil b ve şekil c de görüldüğü gibi her bir kaynağın etkisi ayrı ayrı bulunur, daha sonra bunlar birleştirilir. İlk olarak V1 kaynağının etkisini bulabilmek için şekil b de görüldüğü gibi V2 kaynağı uçları kısa devre edilir. Böylece V2 kaynağının uçlarının kısa devre edilmesiyle, R1 direnci doğrudan b noktasıyla şaseye bağlanmış olur. Bunun sonucunda, R2 ve R1 dirençleri birbirine seri bağlı hale gelir ve bu iki direnç V1 kaynağının uçlarına bağlıdır. Böylece bu iki direnç bir gerilim bölücü olur. Sonuç olarak da aranan P noktasındaki gerilim aynı zamanda R1 direnci uçlarındaki gerilimdir.V1 kaynağı tarafından beslenen bu devrede R1 uçlarındaki gerilim VR1‘i bulmak için gerilim bölme yöntemiyle,
VR1 = (R1 / (R1 + R2 )) . V1
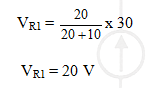
olur.
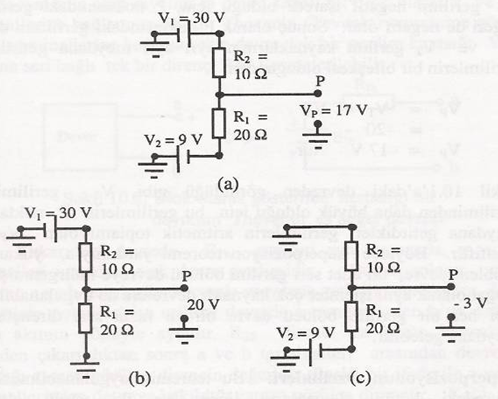
Şekil : İki kaynaklı bir devreye Süperpozisyon teoreminin uygulanması
İkinci olarak, V2 gerilim kaynağının etkisi bulunur. Bunun için yukarıdaki şekilde gösterildiği gibi V1 gerilim kaynağı uçları kısa devre edilir. Yani R2 direncinin üst ucu topraklanır. Böylece, yine R1 ve R2 dirençleri seri olarak V2 kaynağının uçlarına bağlı olduğundan; P noktasındaki gerilim R2 direncinin alt ucundaki gerilime eşittir. Sonuç olarak devre, negatif beslemeli bir gerilim bölücü devre durumuna indirgenmiş olur. Gerilim bölme kuralı uygulanarak VR2 gerilimi bulunabilir. Yani
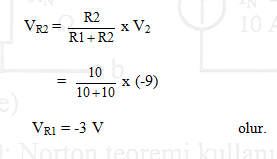
V2 gerilimi negatif işaretli olduğu için, P noktasındaki gerilimin değeri de negatif olur. Sonuç olarak P noktasındaki gerilimin değeri V1 ve V2 gerilim
kaynaklarının ayrı ayrı meydana getirdikleri gerilimlerin bir bileşkesi olduğundan,
VP = V1 + V2
= 20 – 3
VP = 17 V ‘tur.
Yukarı şekildeki devreden görüldüğü gibi, V1 gerilimi V2 geriliminden daha büyük olduğu için bu gerilimlerin P noktasında meydana getirdikleri gerilimlerin aritmetik toplamı olan Vp de pozitiftir. Böylece Süperpozisyon teoremi yardımıyla, yukarıdaki problem devre, iki adet seri gerilim bölücü devreye indirgenmiş olur. Doğal olarak aynı işlemlerden çok kaynaklı devrelere de uygulanabileceği gibi her bir gerilim bölücü devre birden fazla seri dirençten de meydana gelebilir.
Süperpozisyon’un Özellikleri :
Bu teoremin uygulanabilmesi için devredeki bütün elemanların lineer ve iki yönlü olmaları gerekmektedir. Herhangi bir elemanın lineer olması demek, o elemana uygulanan gerilim ile içinden geçen akımın orantılı olması demektir.Elemanın iki yönlü olması ise eleman uçlarına uygulanan gerilim işareti değişse bile içinden geçen akım miktarının değişmemesidir. Elektrik devrelerinde, dirençler, kapasitörler ve hava nüveli (çekirdekli) bobinler genellikle lineer ve iki yönlü elemanlardır. Bu elemanlar aynı zamanda pasif olup yükseltme ya da doğrultma yapmazlar.Yarı iletken diyot, transistor gibi elemanlar, genellikle lineer değildir ve bir yönlüdür.
Örnek :
Aşağıdaki elektrik devresinde, kol akımlarını ve AAB gerilimlerini Süperpozisyon yöntemi ile bulunuz.
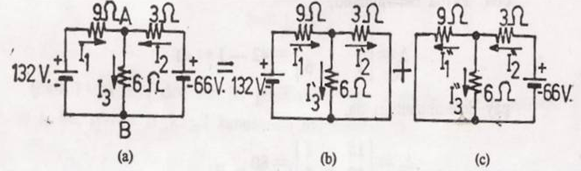
Çözüm :
Yukarıdaki şekildeki devreyi önce 132 V. luk kaynağın beslediği kabul edilir. 66 V. luk kaynak devreden çıkarılarak, açılan uçlar, kısa devre edilir. Böylece elde edilen şekil b deki devre de I1‘, I2‘, I3‘ akımları hesaplanır. Kaynağın verdiği akım,

Böylece her bir kaynağın devreyi ayrı ayrı beslemesi halinde, kollardan geçirecekleri akımlar bulundu. Şimdi her iki batarya devrede bulunduğuna göre kol akımları,
I1 = I1‘ – I1” = 12 – 4 = 8 A.
I2 = I2” – I2” = 10 – 8 = 2 A
I3 = I3‘ + I3” = 4 + 6 = 10 A.
olur. Sonucun doğruluğunu kontrol için A noktasına Kirşofun akımlar kanunu uygulanırsa,
Ia = I1 + I2 = 8 + 2 = 10 A.
Olarak bu kanunun sağlandığı görülür. UAB gerilimi ise,
UAB = 6 . I3 = 6 . 10 = 60 V.
bulunur.
Kaynak: İsmail ÇOŞKUN – Emin GÜVEN – ELEKTROTEKNİK
belgesi-2879